Mazda CX-30 Price Data - Modelling

Modelling car price data with linear regression and regression trees to understand what influences car price depreciation.

CarPrice

Mazda CX-30

Author

John Bates

Published

April 5, 2023

Given the cleaned dataset that we created in the companion notebook Car Price Data - Preparation we now want to attempt to obtain some numerical estimates of how different variables affect the monthly car price depreciation. As in the previous notebook we will be using the tidyverse packages.

We start by reading in the cars tibble that we created and saved.

library(tidyverse)
cars <- readRDS("../01.preparation/mazda.rds")

We restrict its content to used “Used” cars. And we restrict its content to cars for which we have a value for depreciation_per_month.

cars <- cars |>
  filter(new_used == "Used") |>
  filter(!is.na(depreciation_per_month))

We ended the visualisation notebook with a table of monthly median depreciation values for each combination of variant, engine and drive.

These are ordered in ascending order of the median depreciation per month.

cars |>
  select(depreciation_per_month, variant, engine, drive) |>
  group_by(variant, engine, drive) |>
  summarise(n=n(), median_dpm = median(depreciation_per_month)) |>
  arrange(median_dpm) |>
  knitr::kable(digits=0)

variant	engine	drive	n	median_dpm
SE-L Lux	e-Skyactiv G	2WD	48	186
SE-L	e-Skyactiv G	2WD	32	195
SE-L Lux	e-Skyactiv X	2WD	27	218
Sport Lux	e-Skyactiv G	2WD	88	223
GT Sport	e-Skyactiv G	2WD	27	233
Sport Lux	e-Skyactiv X	2WD	89	241
GT Sport Tech	e-Skyactiv G	2WD	13	252
GT Sport	e-Skyactiv X	2WD	60	253
GT Sport Tech	e-Skyactiv X	2WD	82	285
GT Sport	e-Skyactiv X	AWD	12	304
GT Sport Tech	e-Skyactiv X	AWD	13	306

The difference in depreciation between the 2WD SE-L Lux with the e-Skyactiv G engine and the top of the range AWD GT Sport Tech with the e-Skyactiv X engine is about £120 per month. So we can see that these variables clearly have an influence on the depreciation but we would like to know just how much that influence it.

One method available to us is to perform a linear regression of our independent variables (variant, engine, drive, age_in_months and miles_per_month) on our dependent variable depreciation_per_month.

There are several assumptions made when using linear regression:

The independent variables are truly independent of each other: This is a reasonable assumption here, especially after we converted depreciation to depreciation_per_month and miles to miles_per_month thereby removing a dependency on age_in_months.
There are no outliers: We will ensure that below.
The variables are normally distributed: This one is a little more tricky. Some are, some not so much.
There is a linear relationship between the independent variables and the dependent variable: An assumption that we will make based on the scatter-plots of the previous notebook.

A pairs.panels plot from the psych library confirms that the correlations between the independent variables are low.

library("psych")
pairs.panels(
  cars[c( "variant", "drive", "engine","age_in_months", "miles_per_month")],
  cor=T
)

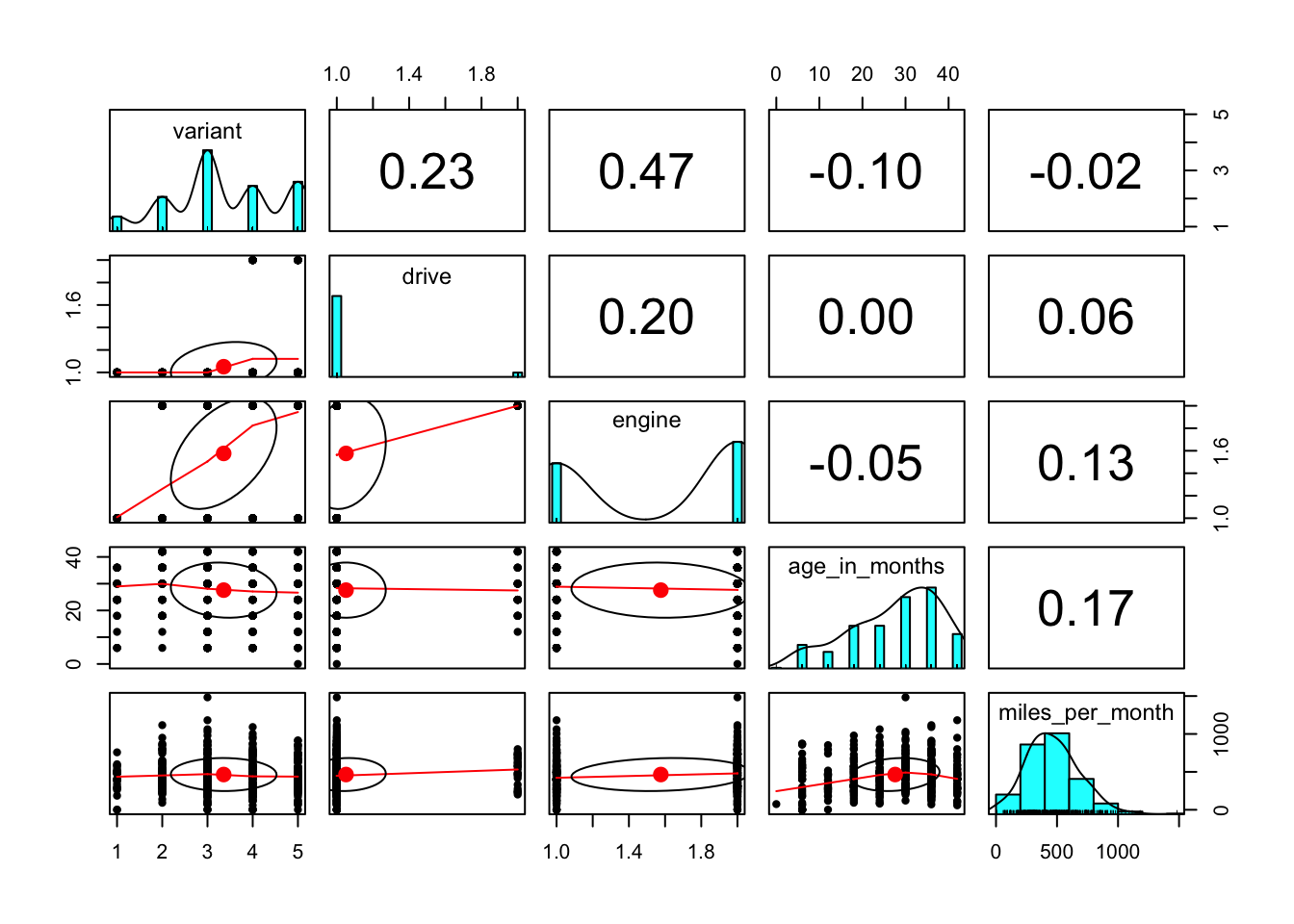
We should also consider removing outliers from our analysis. The outliers are the observations that lie beyond the extremes of the whiskers in a box and whiskers plot. That is, those observations that are more than 1.5 times the interquartile range above or below the 75% and 25% quartiles.

We can see the outliers on the boxplot.

ggplot(
    data = cars,
    mapping = aes(x = depreciation_per_month)
) + geom_boxplot()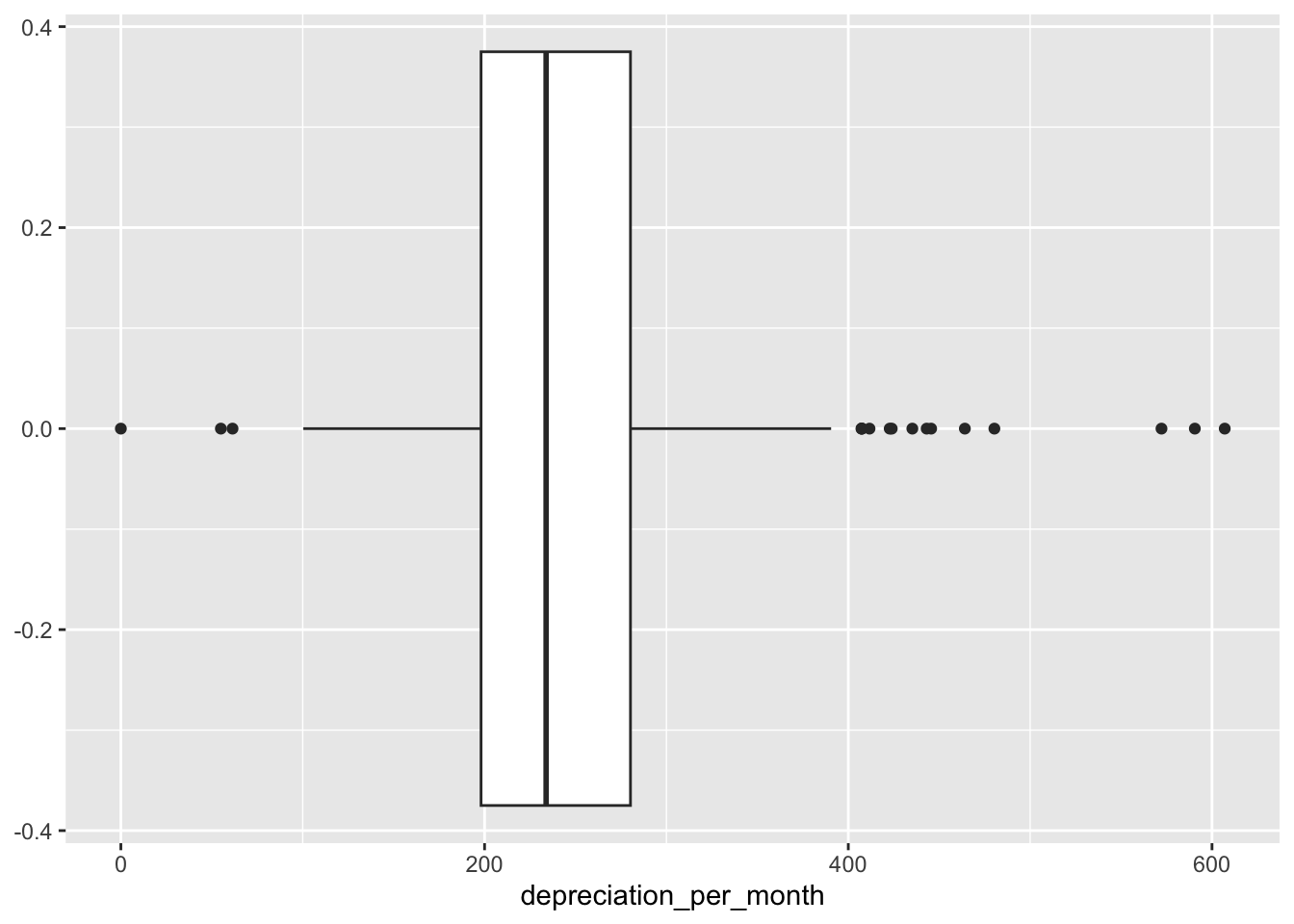

These can be captured and removed by calculating the interquartile range and the 25% and 75% quantiles.

iqr <- IQR(cars$depreciation_per_month)

q25 = quantile(cars$depreciation_per_month, 0.25)
q75 = quantile(cars$depreciation_per_month, 0.75)
lower <- q25 - 1.5*iqr
upper <- q75 + 1.5*iqr

outliers <- cars |>
  filter(
      depreciation_per_month > upper
    | depreciation_per_month < lower
  )

We can examine the outliers by variant, engine and drive and then calculate their median depreciation_per_month (dpm), depreciation (d) and age_in_months (a).

outliers |>
  select(
    depreciation_per_month, variant, engine, drive,
    depreciation, age_in_months
  ) |>
  group_by(variant, engine, drive) |>
  summarise(n=n(),
    dpm = median(depreciation_per_month, na.rm=T),
    d=median(depreciation, na.rm=T),
    a=median(age_in_months, na.rm=T)
  ) |>
  arrange(dpm) |>
  knitr::kable(digits=0)

variant	engine	drive	n	dpm	d	a
Sport Lux	e-Skyactiv G	2WD	2	249	4900	12
GT Sport	e-Skyactiv X	2WD	5	407	3665	6
GT Sport Tech	e-Skyactiv X	AWD	1	407	8556	18
GT Sport	e-Skyactiv G	2WD	1	412	3705	6
GT Sport Tech	e-Skyactiv G	2WD	2	423	3810	6
Sport Lux	e-Skyactiv X	2WD	1	446	4010	6
GT Sport	e-Skyactiv X	AWD	1	480	7205	12
SE-L Lux	e-Skyactiv G	2WD	2	518	7448	12
GT Sport Tech	e-Skyactiv X	2WD	2	599	3568	3

We notice that the outliers look to be mainly from the very expensive combinations of variant and engine and so it may really be that they were highly depreciated vehicles. We could choose to leave these outliers in for the analysis and treat them as valid observations. But given that they are quite small in number we will remove them.

cars <- cars |>
  filter(
      depreciation_per_month < upper
    & depreciation_per_month > lower
  )

Linear Regression

To estimate the numeric effect of each of our independent variables on the value of the dependent depreciation_per_month variable we can perform a linear regression on the data.

A linear regression will fit a straight line through the data of the form:

\[ depreciation\_per\_month = \alpha + \beta_1 * variant + \beta_2 * engine + \beta_3 * drive ... \]

We will be interested in the value of \(\alpha\), and the accompanying \(\beta\) values. The constant value \(\alpha\) will give us the base monthly depreciation and the the \(\beta\)s will give us the amount by which the predicted monthly depreciation will be increased (or decreased) when a vehicle has the associated variant, engine size or drive. Or in the case of the continuous independent variables, how much the predicted monthly depreciation will increase with each month of age or mile of travel of the vehicle.

To handle the independent variables that are factors, the model will employ dummy coding to convert each value of the factor into a numeric variable that takes on the value zero or one according as the observation takes on that value of the factor. When performing this conversion the first level of the factor is left out as it represents the situation when all of the other dummy coded factor values for that factor take on the value zero. This will be a little clearer when we look at the results of the regression.

model.lm <- lm(
  depreciation_per_month ~
    variant+engine+drive+age_in_months+miles_per_month,
  data=cars
)
summary(model.lm)


Call:
lm(formula = depreciation_per_month ~ variant + engine + drive + 
    age_in_months + miles_per_month, data = cars)

Residuals:
     Min       1Q   Median       3Q      Max 
-136.530  -14.875    0.466   19.318  124.951 

Coefficients:
                       Estimate Std. Error t value Pr(>|t|)    
(Intercept)          236.784458   6.777371  34.938  < 2e-16 ***
variantSE-L Lux       36.073971   6.607608   5.459 7.79e-08 ***
variantSport Lux      38.310408   6.008123   6.376 4.38e-10 ***
variantGT Sport       60.552317   6.605046   9.168  < 2e-16 ***
variantGT Sport Tech  78.190497   6.737117  11.606  < 2e-16 ***
enginee-Skyactiv X     1.360104   3.230797   0.421    0.674    
driveAWD              47.097788   6.695771   7.034 7.22e-12 ***
age_in_months         -3.312248   0.146638 -22.588  < 2e-16 ***
miles_per_month        0.093089   0.006535  14.244  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 29.95 on 465 degrees of freedom
Multiple R-squared:  0.6921,    Adjusted R-squared:  0.6868 
F-statistic: 130.6 on 8 and 465 DF,  p-value: < 2.2e-16

The residuals in the output are an indication of how well (or badly) our model fits the observed values of depreciation_per_month. The first thing to notice is that the maximum and minimum values of the residuals are £124 and -£136 respectively. These are the worst cases. The 50% of observations that fall between the 1Q and 3Q values have residuals that range between -£14 and £19. That seems like a very comfortable range.

Before examining the fitted values we need to look at the goodness of fit. The Adjusted R-squared value of 0.6868 is good. This value gives us an indication of how well our model explains the variation in monthly depreciation - in this case approximately 68%.

We also see that the three stars against each of the independent variables (except for engine) tell us that it is extremely unlikely that they do not influence the value of our modelled dependent variable, depreciation_per_month.

We can plot the residuals against the fitted values of the model:

predicted <- predict(model.lm)
residuals <- residuals(model.lm)
ggplot(
    data = cars,
    aes(x = predicted, y = residuals)
) + geom_point()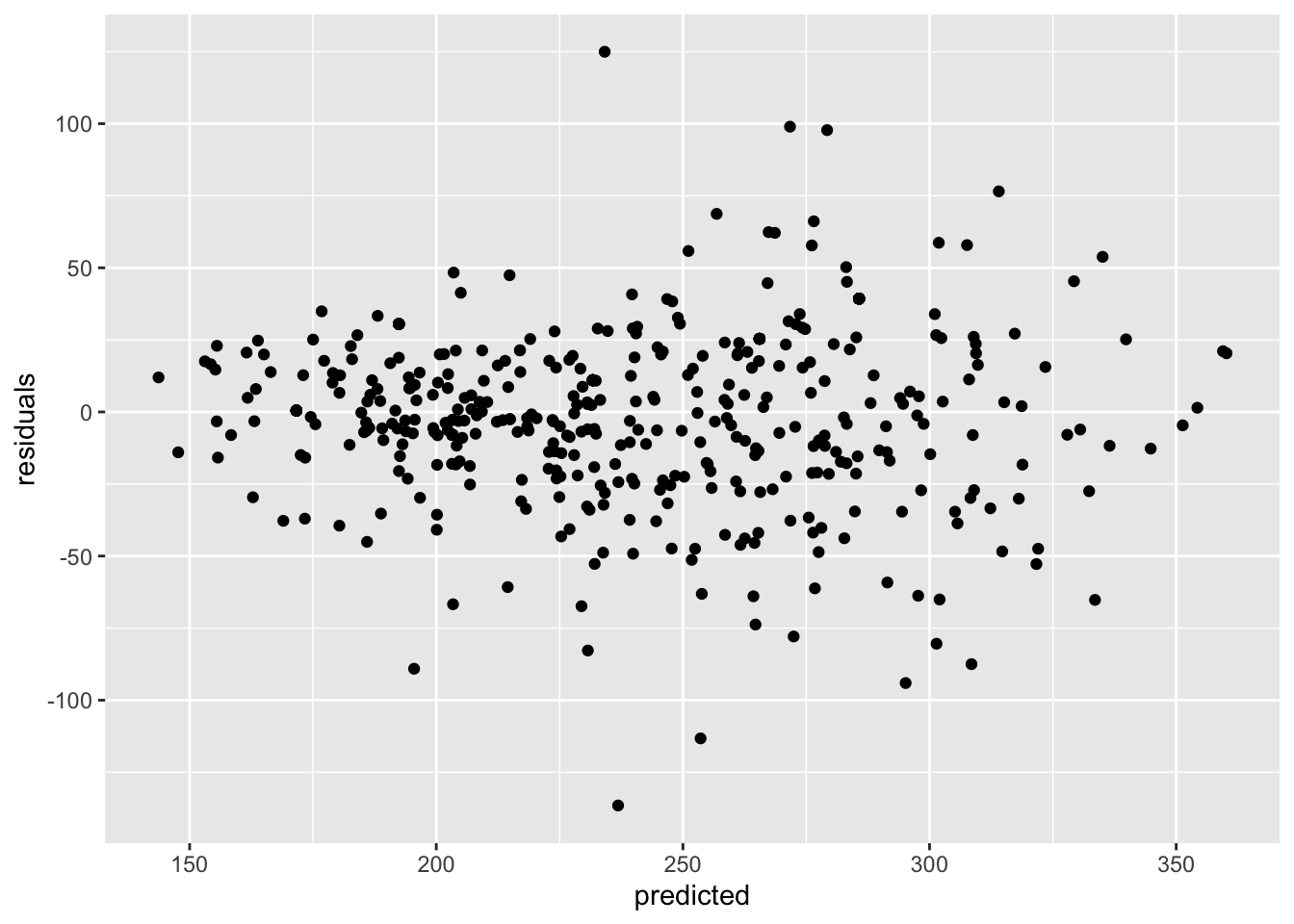

This seems like a reasonable spread, perhaps slightly wider towards the higher end of the predicted values but good enough. Given that we are happy with the fit of the model we can now look at the values of the various fitted coefficients.

Before we can do that though we need to understand how the non-numeric (nominal) dependent variables in our model are handled by the regression. We can see that:

For our 5 level variant variable the model contains 4 parameters: variantSE-L Lux, variantSport Lux, variantGT Sport, variantGT Sport Tech.
For our 2 level engine variable the model contains a single parameter: enginee-Skyactiv X.
For our 2 level drive variable the model contains a single parameter: driveAWD.
For our numeric age_in_months variable the model contains a single parameter: age_in_months.
For our numeric miles_per_month variable the model contains a single parameter: miles_per_month.

The key thing to note is that each non-numeric variable (a factor in our dataset) is represented in the model by (n-1) parameters where n is the number of levels of the factor that represents the nominal variable. The regression ensures that the effect of the first of the factor levels is incorporated into the value of the estimated intercept. To see the effect of having one of the other factor levels in an observation we need to add its associated coefficient to the value of the intercept.

For example, to represent the drive factor our model has a parameter driveAWD with a coefficient of (roughly) 47. This tells us that, in general, a vehicle with AWD will depreciate at £47 per month more than a vehicle with 2WD. If we plug the estimated intercept value and the rounded coefficients for the various model parameters into our model equation it looks like this:

  depreciation_per_month = 237
    + 36 * variantSE-L Lux 
    + 38 * variantSport Lux
    + 61 * variantGT Sport
    + 70 * variantGT Sport Tech
    + 47 * driveAWD
    - 3 * age_in_months
    + 0.09 * miles_per_month

We have omitted the engine parameter from this model because the regression analysis determined that it has an insignificant effect on the monthly depreciation.

The intercept value of £237 can be considered to be the estimated monthly depreciation of a vehicle with variant=SE-L, drive=2WD, age_in_months=0 and miles_per_month=0.

Were we to replace our variant SE-L with a variant of GT Sport then we should expect our monthly depreciation to increase by £61. If we then further opted for 4WD we could add another £47 onto the estimated monthly depreciation.

Similarly for the numeric parameters, if we were to consider the same specification at 12 months old we would subtract 12 * £3 = £36 from the estimated monthly depreciation. And 1,000 mile per month of travel would add £90 onto the estimated monthly depreciation.

So the regression gives us a very understandable explanation of how much each of the independent variables affects the value of the monthly depreciation.

Regression Trees

An alternative to using linear regression to model our data is to use regression trees. A regression tree model is built by splitting the set of observations into two partitions in such a way as to maximise the reduction in variation between the observations that lie within each partition. This requires both a choice of feature to split on and then a value with which to partition the data on that feature.

For example, if the miles_per_month feature is chosen as the one that can maximise the reduction in variation, it might then be determined to partition the data into two sets: one whose miles_per_month value was >1000 and one whose miles_per_month value was <= 1000.

This gives us two nodes of a tree. Then the procedure is repeated on the data in each node, giving us four nodes, and so on until there is no significant reduction to be obtained by splitting further.

Once the tree has been constructed by repeating the above process we have:

A set of rules that result in a path to each of the leaf nodes.
A set of homogeneous data in each node from which a mean value of the dependent variable depreciation_per_month can be determined.

For a new observation we can follow the set of rules until we arrive at a leaf node and then we can use the mean value of monthly depreciation of observations in that node as our estimate of the monthly depreciation of the new observation.

To build a regression tree we use the “rpart” package and its associated plotting package.

library(rpart)
library(rpart.plot)

We will build a regression tree model using the same variables that we used for the linear regression model.

model.rt <- rpart(
  depreciation_per_month ~
    variant+drive+engine+age_in_months+miles_per_month,
  data = cars
)

A good visual representation of the regression tree can be obtains by using rpart.plot.

rpart.plot(model.rt)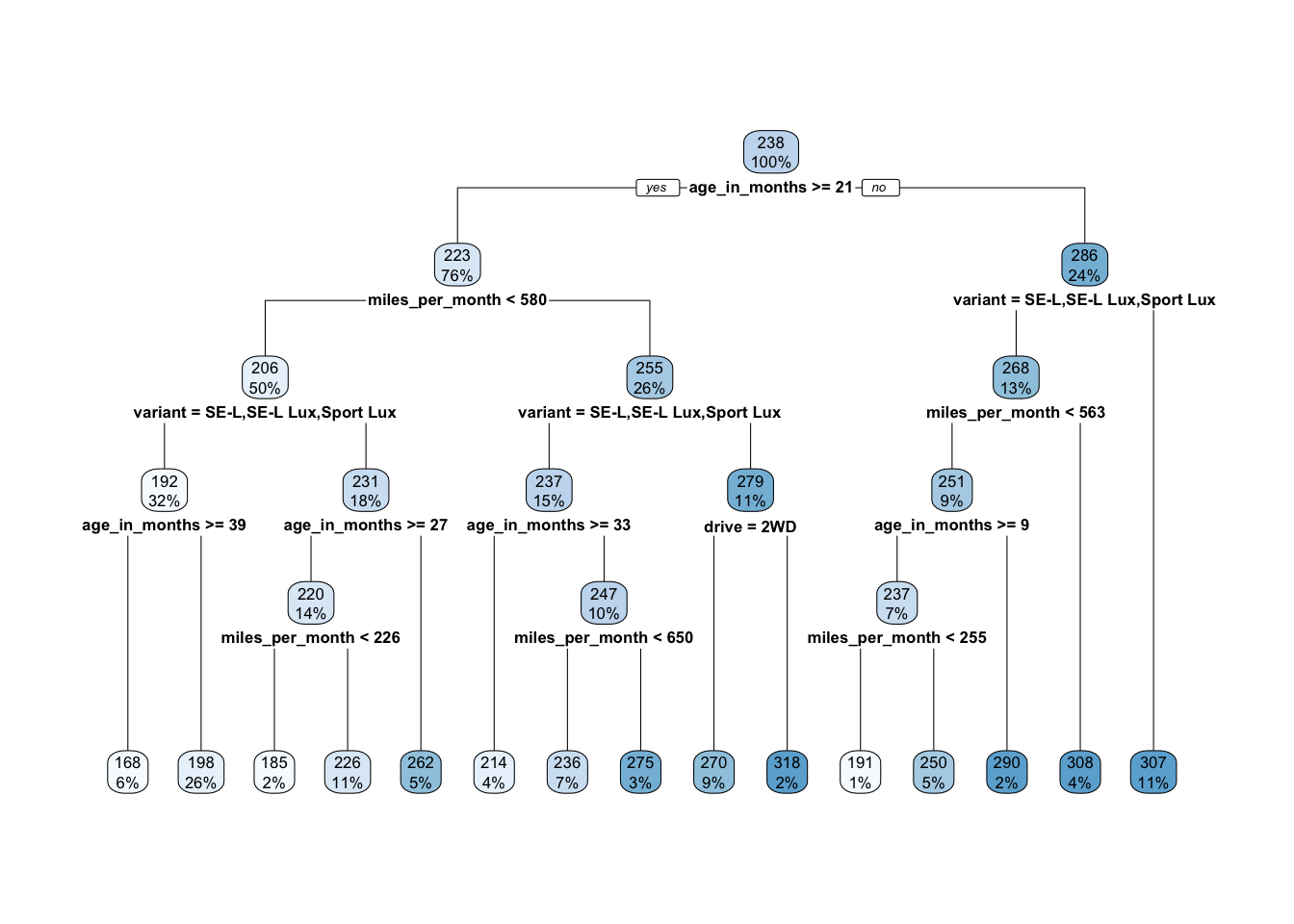

We can see that the first variable that was split was age_in_months and that the resulting tree has five levels and terminates in 15 leaf nodes. The values within each node are the mean depreciation_per_month of the observations that fall into that node and the percentage of the observations that reach that point.

Because age_in_months was used first in the tree it is the single most important predictor of the monthly depreciation of a vehicle. The regression model divides the observations on age_in_months >= 21, placing all observations for which this is true in the node on the left-hand-side of the split and all other observations in the node on the right-hand-side.

We can repeat this process right the way down the tree. If we consider the observations for which age_in_months is not greater than 21 (i.e. relatively new vehicles) then the next best predictor of monthly depreciation is variant. This node tells us that for the cheapest variants (SE-L, SE-L Lux and Sport Lux) the next best predictor is miles_per_month otherwise the model takes us straight to a leaf node with an estimate of monthly depreciation of £307.

We can get a feel for how good our model is by calculating the mean absolute error.

MAE <- function(actual, predicted) { mean(abs(actual - predicted))}

Normally we would have divided our observations up into a training set and a testing set to perform this operation but here we will use mean absolute error to get a feel for how closely this model can predict our observed monthly depreciation.

predicted = predict(model.rt, cars)
actual = cars$depreciation_per_month

print(MAE(actual, predicted))

[1] 22.85299

So, on average, our model predicts the value of the monthly depreciation to within £23 of the observed depreciation. We could think of that as a measure of what we have lost by summarising the data into a structured and explainable model.

Let us look at what we would have obtained had we trained our model on a proportion of the data and then used the remaining observations to test its predictive accuracy.

We use set.seed to ensure that our results are reproducible. We take a random selection of 90% of our observations for the training set and use the remaining 10% to test the resulting model.

set.seed(15151)
n <- (cars |> count())[[1]]
cars_rand <- cars[order(runif(n)),]
split <- round(n*0.9, 0)

cars_train <- cars_rand[1:split, ]
cars_test <- cars_rand[(split+1):n, ]

model.rt.train <- rpart(
  depreciation_per_month ~ variant+drive+engine+age_in_months+miles_per_month,
  data = cars_train
)

We can plot the decision tree of the training model as we did for the model we obtained from the full set of data.

rpart.plot(model.rt.train)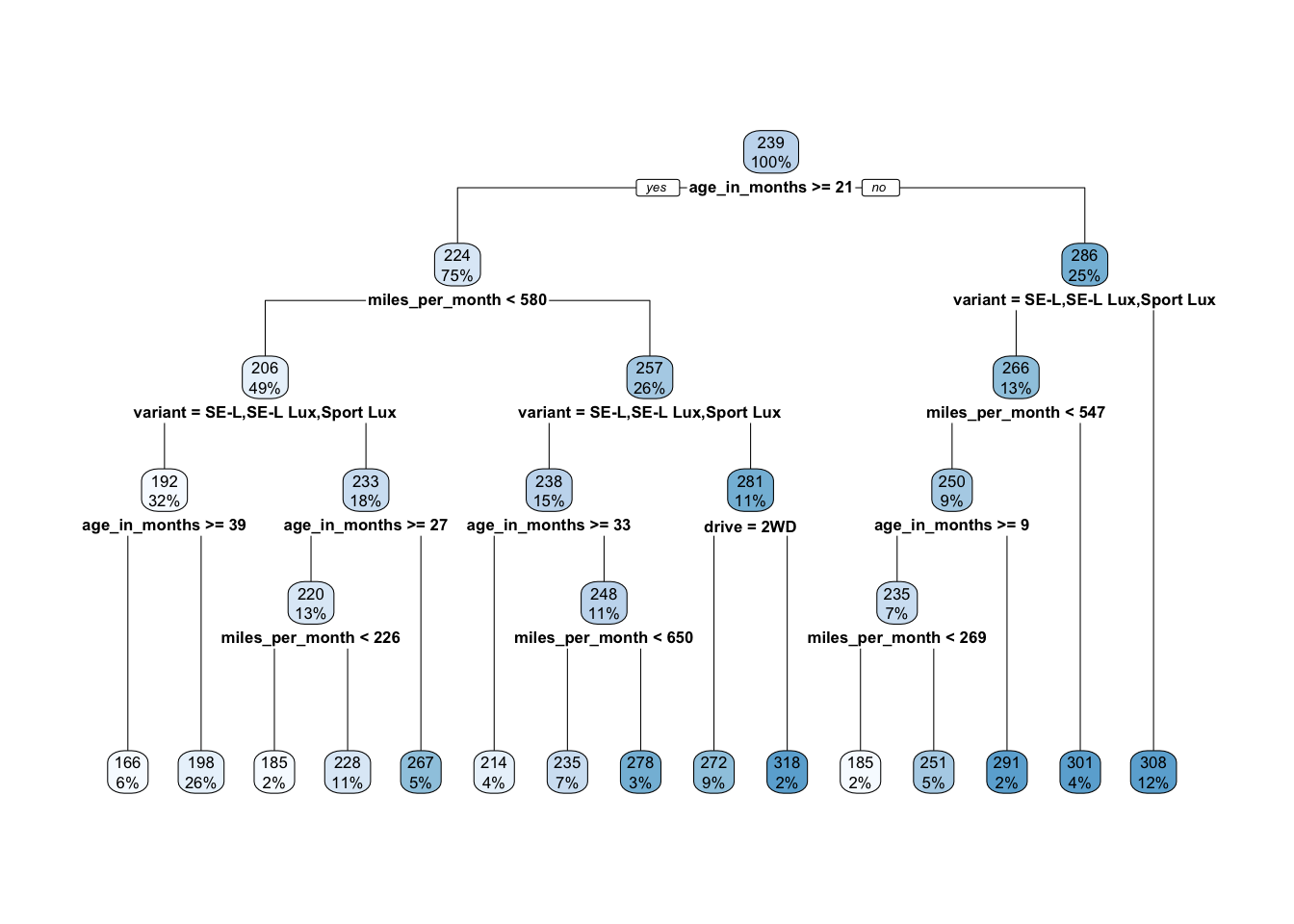

Perhaps unsurprisingly, but somewhat reassuringly, the tree is almost identical to the previous one. The choice of variable to split on is unchanged at each point in the tree and the numerical splits differ very slightly in just two places. It feels as though the structure of the tree is quite stable.

predicted = predict(model.rt.train, cars_test)
actual = cars_test$depreciation_per_month

print(MAE(actual, predicted))

[1] 25.53228

As we would expect, the mean absolute error is slightly higher than the value that we obtained using the data that the model was trained on. Nevertheless this seems like a very small value for error in monthly depreciation, which suggests that our model is a good one.

We have seen how a regression tree can provide an alternative mechanism for understanding what drives monthly depreciation in our car dataset.

Linear Regression vs Regression Tree

We can compare the linear regression and the regression tree by training a new linear regression model on our training set and then calculating the mean absolute error of its predictions using the test data.

model.lm.train <- lm(
  depreciation_per_month ~ variant+engine+drive+age_in_months+miles_per_month,
  data=cars_train
)

summary(model.lm.train)


Call:
lm(formula = depreciation_per_month ~ variant + engine + drive + 
    age_in_months + miles_per_month, data = cars_train)

Residuals:
     Min       1Q   Median       3Q      Max 
-134.812  -14.294    0.223   19.508  124.575 

Coefficients:
                       Estimate Std. Error t value Pr(>|t|)    
(Intercept)          236.182614   7.181542  32.887  < 2e-16 ***
variantSE-L Lux       35.813388   7.004416   5.113 4.84e-07 ***
variantSport Lux      36.963980   6.406757   5.770 1.55e-08 ***
variantGT Sport       60.524787   7.045595   8.590  < 2e-16 ***
variantGT Sport Tech  80.297976   7.209481  11.138  < 2e-16 ***
enginee-Skyactiv X     1.417235   3.420915   0.414    0.679    
driveAWD              45.502400   6.776377   6.715 6.16e-11 ***
age_in_months         -3.298002   0.153850 -21.437  < 2e-16 ***
miles_per_month        0.094333   0.006905  13.661  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 30 on 418 degrees of freedom
Multiple R-squared:  0.6999,    Adjusted R-squared:  0.6941 
F-statistic: 121.8 on 8 and 418 DF,  p-value: < 2.2e-16

A look at the model parameters confirms that it has hardly changed from the model that was fitted on the full set of data.

predicted.rt = predict(model.rt.train, cars_test)
predicted.lm = predict(model.lm.train, cars_test)

print(str_glue(
  "MAE of regression tree:",
  round(MAE(actual, predicted.rt),2))
)

MAE of regression tree:25.53

print(str_glue(
  "MAE of linear regression:",
  round(MAE(actual, predicted.lm),2))
)

MAE of linear regression:23.38

The errors are almost identical, with the linear regression slightly out performing the regression tree.

We now have two useful models of monthly depreciation that can be used to examine what drives depreciation on used Mazda CX-30 cars in the UK.

In the next notebook we will look at a mechanism for creating a simple two-dimensional table to display aggregated car price data.

Next: Mazda CX-30 Price Data - Tabulation