Drawdown_Ivy: An Ivy tool to Model Pension Drawdown
Drawdown_Ivy is an Ivy tool to model retirement pension drawdown and the influence of external factors on its duration, expected remainder (if any), and the amount lost to taxes.
Drawdown_Ivy is an Ivy script to model retirement pension drawdown. It is a slightly simplified implementation (in Ivy) of the Drawdown tool that I previously implemented in Go, and which is described here.
Apart from the implementation language, the biggest difference between the Ivy drawdown tool and the Go drawdown tool is that the Go tool has the ability to model more complex income sources. It also has the ability to pay taxes within the year in which they are raised. The Ivy tool accumulates a value for the taxes due and adds that value onto the amount needed the following year. I have since added an option to allow the Go tool to do this as it seems to more closely match our behaviour in real life.
The Ivy code for Drawdown_Ivy can be found on GitHub here.
Usage
ivy ./drawdown.ivyThe program will print its results in CSV format to standard output. The output is largely the same as the un-summarised output of the Go implementation of the drawdown tool and its examples of output in Normal Mode give an indication of what could be created from this output.
Microsoft Excel is a good tool for viewing the output. In particular, a pivot table and pivot chart give a good visualisation of how things are changing from year to year.
A stacked bar chart (Figure 1) can be used to show the makeup of each yearly withdrawal.
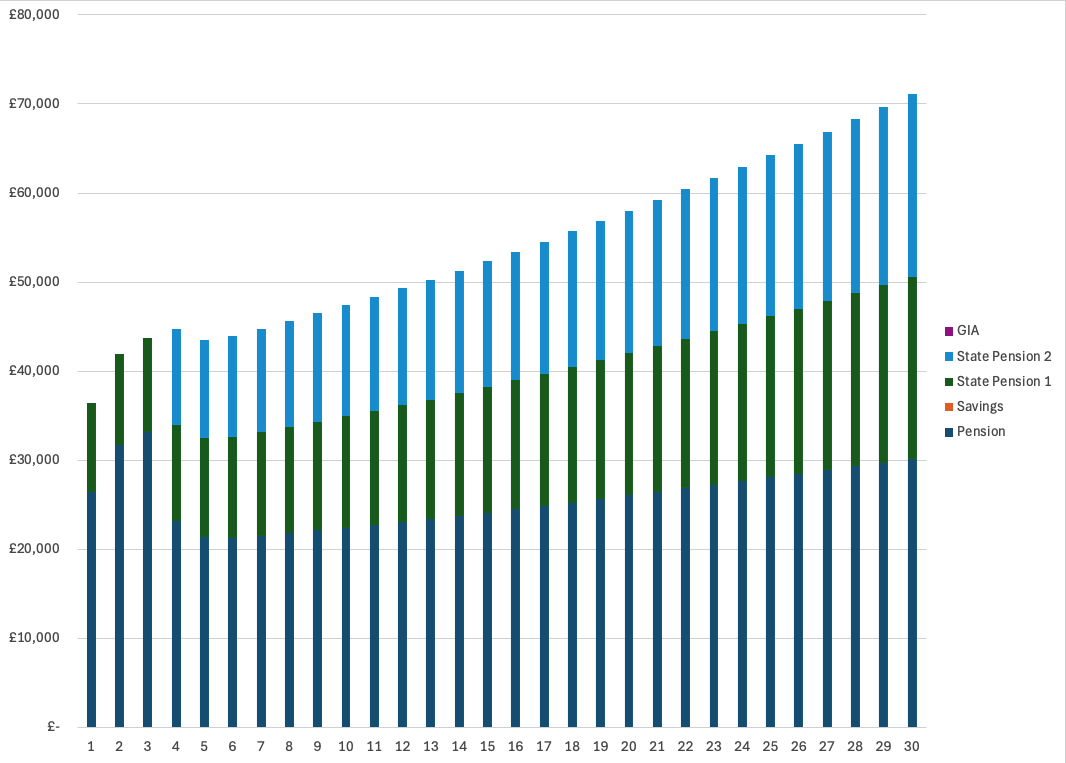
In this example you can see that, state pension 2 kicks in in year 4 and that, in addition to the two state pensions, we are drawing from our private pension but not the general investment account or our savings.
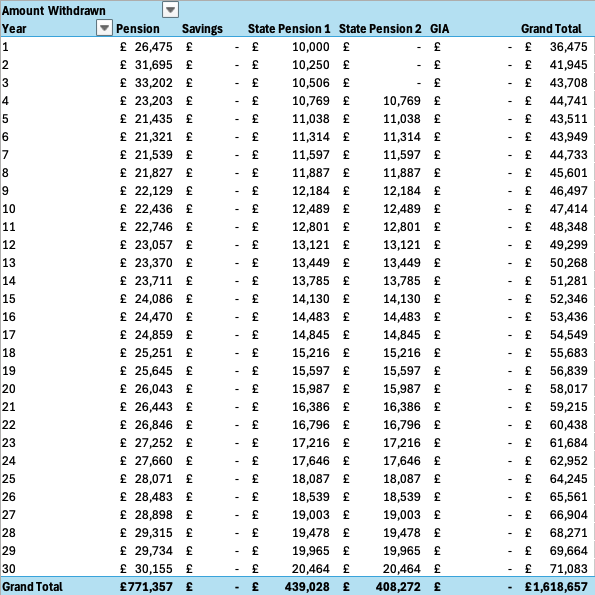
The tabular view (Figure 2) gives an alternative view of the same data.
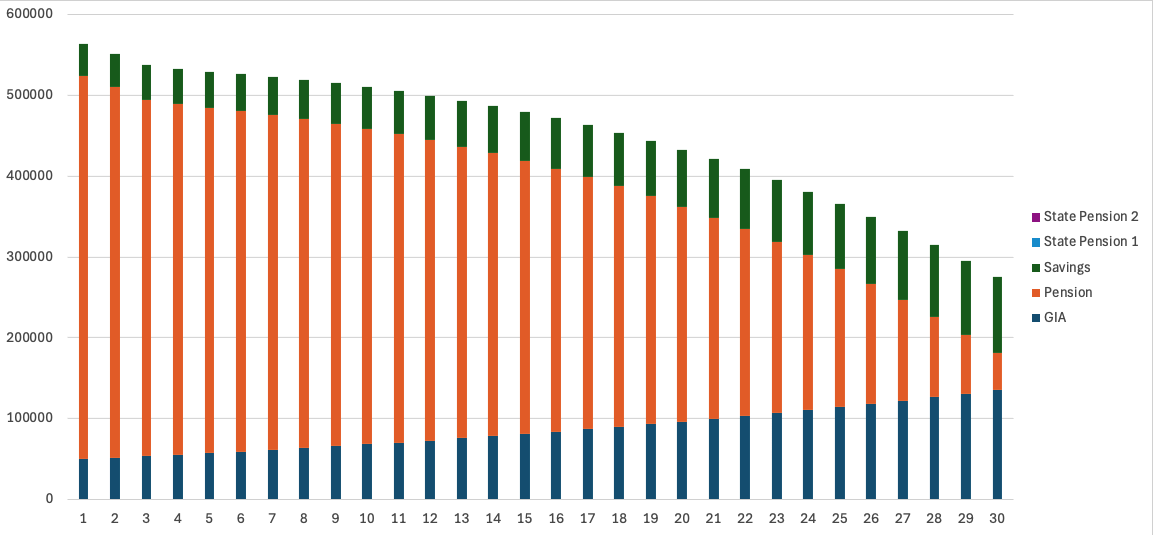
Figure 3 shows how the balance of the non-state pension sources changes over time. Our pension balance is almost depleted after 30 years but, because we are not drawing from them, our savings and general investment account balances continue to grow.
This Ivy implementation is simpler in its aims (than the Go implementation) but is still a useful tool for investigating the effect of environmental conditions on a pension pot. This document describes the implementation (mostly) for my own benefit.
The Ivy implementation is considerably shorter in terms of the number of lines of code when compared to the Go implementation. Even though a seasoned Ivy programmer would consider my coding style to be far from terse, and I almost certainly fail to spot several coding idioms that would result in more compact code, the Ivy implementation is 170 lines long whereas the Go implementation is just over 1000 lines long.
The remainder of this document annotates the source code.
Constants
There are a number of constants that are defined at, or near, the top of the Ivy script (drawdown.ivy) that are intended to be experimented with.
# Rates. All percentages
Igr = 3.5 / 100 # Investment Growth Rate
Sgr = 3.0 / 100 # Savings Growth Rate
Inf = 2.0 / 100 # Annual Inflation Rate
Pcr = 0.25 / 100 # Platform Charge Rate
Tbr = 0.5 / 100 # Tax Band Annual Percentage Increase
# Starting Parameters
N = 30 # Number of years to iterate.
Year1Income = 35000 # Income to draw each year.Igr and Sgr are the percentage growth rates that are to be assumed will apply over the course of the iterations to investment sources and savings sources. An investment source might be a stocks and shares ISA or a pension fund. A savings source might be a cash savings account or other fixed income instrument, such as a bond. The only real distinction between the two being that you might consider, say, the investment source to have a higher likely annual growth rate than a savings source.
Inf allows a figure to be given for the expected average annual percentage inflation rate over the whole period. Each year the iterations will increase the needed amount of income by this percentage.
Pcr determines the amount of platform charge that is paid each year. Before any withdrawals are made from the sources a platform charge is added to the needed amount of income. The amount of the platform charge is Pcr percent of the remaining asset value at the start of the year. In calculating this asset value we ignore any state pension sources - we assume that they have no platform charge levied on them.
When calculating the tax to be paid each year we consider the tax regimes that are associated with each kind of source. A tax regime, such as capital gains tax or income tax, has a sequence of monetary bands and a percentage tax rate associated with each band. In order to reflect the fact that these bands might increase in value over the years we scale them up by a percentage equal to Tbr at the end of each year.
The constant N determines the number of years over which we will iterate. Our output will contain year end values for each year from 1 to N.
Year1Income is the amount of income that we would like to draw in the first year of the iteration. At the start of each subsequent year this amount will be scaled up by the rate of inflation, Inf. This amount, to which we add any unpaid tax from the previous year and our platform charges, forms the amount of needed income that we will withdraw from the various sources.
Tax Regimes
# Tax Regimes:upper bound and percentage rate
IncReg = (12540 0.0) (50270 20.0) (125140 40.0) (100000000 45.0)
CapReg = (3000 0.0) (100000000 18.0)A tax regime is implemented as an array of pairs of values. Each pair contains an upper bound amount and a percentage rate. The pairs are assumed to be in order of increasing upper bound amount. Together these pairs form a sequence of tax brackets within which the associated percentage of tax will be charged. For example, the income tax regime above IncReg consists of four bands:
- £0 to £12,540 at which no tax will be charged.
- £12,541 to £50,270 at which tax will be charged at the rate of 20%.
- £50,271 to £125,140 at which tax will be charged at the rate of 40%.
- £125,141 and above at which tax will be charged at the rate of 45%.
The “and above” bit is represented by the use of a very large upper bound.
Tax Accounts
# Tax Accounts: Tax Regime, taxed amount, tax
IncT = IncReg 0 0
IncT2 = IncReg 0 0
CapT = CapReg 0 0
TA = IncT IncT2 CapT # Tax AccountsA tax account is associated with each taxable source. A tax account contains three pieces of information:
- The tax regime to use when calculating tax on income drawn from sources that use this tax account.
- The amount, within the current year, on which tax has already been calculated for sources that use this tax account.
- The amount, within the current year, of tax that has been calculated for sources that use this tax account.
A tax account may be shared between more than one source. For example, a state pension source might share the same tax account as a private pension source so that, when calculating income tax, the income drawn from each source is combined.
The global array TA contains the complete set of tax accounts in use by the program. This is initialised using IncT, IncT2 and CapT as templates.
Sources
Sources are perhaps the central focus of the drawdown program. We model the remaining balance of each of the sources as we make annual withdrawals, and as the assets within each source increase in value each year.
# Sources
S = ("State Pension 1" "State Pension 2" "Savings" "Pension" "GIA") # Source names
B = 0 0 40000 500000 50000 # Opening balance
TAI = 1 2 0 1 3 # Index into Tax Accounts, 0 if non-taxable
# Source flags
IsInv = 0 0 0 1 1 # Is an investment source
IsSav = 0 0 1 0 0 # Is a savings source
IsSP = 1 1 0 0 0 # Is source a state pensionThe global array S contains the names of each of the sources that the program will consider. Several other global arrays (and indeed local variables to operators) have the same shape (length) as S. Ivy does not allow us to model pointers to elements of the source array so, instead, we work with indexes into it and maintain a number of other arrays that keep the same order as the source array.
The global array B contains the opening balance (opening asset value) of each of the sources in S. The balances are arranged in the same order as the sources in S. So, for example, we can see that we start the iteration with a “Savings” balance of £40,000 (the actual currency is not important, but it is assumed to be the same currency for all sources). We do not consider state pensions to have an opening balance. Instead, we populate the “balance” of a state pension source with a suitably scaled value at the start of each year.
The ith entry in the global array TAI gives the index into the tax account array TA at which the tax account for the ith source can be found. It contains a zero for sources that are non-taxable. For example, to find the tax account for the general investment account source (GIA) we note that the GIA source is in index position 5 of the source array S so we look at the contents of index position 5 in the tax account index array TAI and we find the value 3. This tells us that the tax account to use for the GIA source can be found in index position 3 of the tax account array TA.
The lack of pointers means that we have to be careful to ensure that if we change the ordering of sources in S then we also need to make the same ordering changes in other places.
The global constants IsInv, IsSav, and IsSP are set to 1 (true) for those sources that are investment sources, savings sources or state pension sources respectively, otherwise they contain a 0 in the position that corresponds to a source. You can see that a source is marked as belonging to only one of those categories.
State Pension Sources
We handle state pensions slightly differently to the way in which we handle other sources.
# State Pension Sources
SPStartYear = 1 4 0 0 0 # If a state pension, what is its start year?
SPY1 = 10000 # State Pension Year1 Amount
SPAPI = 2.5/100 # State Pension Annual Percentage IncreaseWe might be modelling the assets of a couple, in which case we might have more than one state pension source and it is quite possible that they do not all come online in the same year. The global array SPStartYear contains the number of the year in which a given state pension source is to come online. It should contain a 0 in the index position for sources that are not state pension sources.
The constant SPY1 contains the annual amount that a state pension will pay in year 1 of the iteration. This amount is scaled up by a percentage governed by the value of the SPAPI constant.
Draw Sequence
# Order by draw sequence
DS = 1 2 3 4 5 # Draw Sequence
S = S[DS]
B = B[DS]
TAI = TAI[DS]
IsInv = IsInv[DS]
IsSav = IsSav[DS]
IsSP = IsSP[DS]
SPStartYear = SPStartYear[DS]This Ivy implementation of the drawdown program will withdraw amounts from the sources in the order in which they are found in the source array S. Because there are several other global arrays that depend on the ordering of the sources in that array there is a mechanism that allows the sequence to be altered safely. The technique is to change the global draw sequence array DS. This array contains the order of indexes into the source array from which withdrawals will be made. As you can see from the code above the implementation of this is to simply reorder the source array and, at the same time, all of the other global arrays that must be kept in step with it.
If, for example, we wanted to preserve our savings and, instead, draw first from our pension and general investment account we could change the draw sequence to do so:
DS = 1 2 4 5 3 # Draw SequenceIn practice you may not need to make any changes here, but at least it identifies those global arrays whose ordering is dependent on the ordering of the source array.
Withdrawals
The withdrawal functions start with a scalar need amount and an array of remaining balances (one for each of the sources and in source order). The need amount is the annual amount that must be supplied from the sources to satisfy the inflation adjusted income requirements, the platform costs and the previous year’s tax costs in the current year. The job of the withdrawal functions is to step through the remaining balance array withdrawing as much as is available from each source until an amount equal in total to need has been found.
# Withdraw upto need (scalar) from the balances starting at the ith balance.
# Return the new balances
op i withdraw (need balances) =
balance = balances[i]
got = 0 max need min balance
(i == count balances) : got
got, (i + 1) withdraw ((need - got) balances)
# Withdraw need (scalar) from the balances returning the new balances
op withdraw (need balances) =
b = 1 withdraw (need balances)
bThe dyadic version of withdraw is passed (an array containing) a scalar need amount and an array of remaining balances in source order as its right hand argument and a starting index into the balance array as its left argument. The balance array is guaranteed to have the same length as the source array. The balance in the ith index of the array is the remaining balance of the source in the ith position of the source array S.
The aim of withdraw is to find an amount equal to need by withdrawing as much as possible from each of the source balances in order. It returns a withdrawal array of length equal to (count S) - (i-1) with the amount in the first position being the amount that is to be withdrawn from the ith source. Here count S is the length of the source array.
The function focuses on the ith balance. The value got is calculated by first taking the minimum of what we need and the available balance. The restriction that got must be positive is there to protect against being called with a negative balance or need.
If i is equal to the length of balances it returns the scalar got. Otherwise it returns the result of catenating the value of got with the result of calling withdraw with an index of (i+1) and a need amount that has been reduced by the amount that we have got from the source in the ith position.
The monadic version of withdraw returns the result of calling this function with an index of 1.
Tax
Given the withdrawal array (which is the amount that we propose to withdraw from each source) the job of the tax operators is to calculate an array of tax amounts that will be raised as a result of withdrawing the amounts w from the sources.
The amount of tax due from a particular source will depend upon the withdrawn amount, the tax regime associated with the tax account that is associated with the source, and also the amount that has previously been withdrawn from other sources using the same tax account. To be able to calculate this latter figure the tax account contains a running total of the amount withdrawn from all of the sources associated with the tax account. This running total is reset at the end of each year.
op second a = 1 take 1 drop a
# Calculate the amount of tax due for the amount 'a'
op tr taxDue a =
u = first@ tr # upper bounds
r = second@ tr # tax rates
ba = (a min u) - (a min -1 drop (0,u)) # amounts in each bracket
t = +/(ba * r/100) # sum of (bracket amount times rate)
t
# Calculate tax on the ith source given w[i] withdrawn.
# Return zero for non-taxable sources.
# The tax account contains the already withdrawn amount from other sources in the same tax account.
# Update the tax account with the amount withdrawn and tax calculated.
op i taxOn ws =
tai = TAI[i] # tax account index
(tai == 0): 0
ta = TA[tai] # tax account
tr = ta[1] # tax regime
w0 = ta[2] # amount that tax has already been calculated on (from other sources)
w = ws[i] # withdrawn amount from this source
t0 = ta[3] # tax already calculated (from other sources)
t = (tr taxDue (w0+w)) - (tr taxDue (w0)) # additional tax
TA[tai] = ta[1] (w + w0) (t + t0) # accumulate taxed amount and tax (raised)
t
# Calculate the tax to pay on each element of w
op taxOn w =
(iota count S) @taxOn w # tax dueThe monadic taxOn operator is called with an array of withdrawals (one for each source). It calls the dyadic taxOn operator with a source index as its left argument.
The dyadic taxOn operator focuses on the ith source. It determines the tax account index by indexing into the tax account index array TAI and so finds the tax account.
From the tax account it extracts the tax regime tr, the amount of withdrawals that we have already calculated tax on using this tax account w0, and the tax that has already been calculated as being due on this tax account from other sources t0.
Then, using the amount that we have withdrawn from this ith source w it calculates the difference between the tax that would be due on a withdrawal of (w0+w) and an amount that would be due on a withdrawal of just w0 - this is the additional tax t.
Finally it updates the tax account with the new values for the amount that has been taxed, w+w0, and the amount of tax raised, t+t0.
The taxDue operator takes a tax regime as its left argument and a scalar amount as its right argument. It returns the scalar amount of tax due, t, as a result of withdrawing the amount a.
It begins by extracting the array of upper bounds, u, and the array of associated tax rates, r from the tax regime.
It calculates the size of each of the tax brackets by subtracting u shifted right by one position (and with a zero prepended) from itself. But by carefully limiting the maximum value of either term to be a it results in an array of values of the same length as u but which contains the amount of a that falls into each bracket, ba.
It is then easy to calculate a scalar tax value by summing over the product of the rate in r and the amount in ba. This value, t, is then returned.
Year Start and Year End
At the start of the year we initialise the state pension balances and scale up the investment and savings balances using the appropriate scaling constants.
# Start year n with balances b.
# Return new balances (after any scaling up)
op startYear (n b) =
ids = iota count b
# set state pensions
i = (IsSP and (n >= SPStartYear)) # identify state pensions
b[i sel ids] = SPY1 * (1 + SPAPI) ** n - 1 # set their scaled up balance
#
# scale up investments and savings (apart from in year 1)
(n == 1): b
b[IsInv sel ids] = b[IsInv sel ids] * 1 + Igr
b[IsSav sel ids] = b[IsSav sel ids] * 1 + Sgr
b
# Reset the counters in the tax account with index 'tai'
op resetAndScaleTaxAccount tai =
ta = TA[tai] # tax account
tr = ta[1] # tax regime
m=mix tr # as an nx2 matrix. first column contains the bands.
m[;1] = m[;1] * 1 + Tbr # scale the bands
tr = split m # return to vector shape
TA[tai] = tr 0 0 # set scaled tax regime, and zero taxed amount and tax counters
op endYear (n b) =
resetAndScaleTaxAccount@ iota count TA
bState pension balances are assumed to be fully withdrawn each year.
At the end of the year we scale the bands in the tax account tax regime up using the appropriate percentage constant and we reset the taxed amount and tax raised counters in the tax account
Yearly Iteration
UnpaidTax = 0
# Iterate year n with starting balance b. Return balance, withdrawals, and tax incurred at year end.
op n year b =
need = Year1Income * (1 + Inf) ** n - 1 # scale by inflation.
need = need + UnpaidTax # add in unpaid tax from the previous year.
UnpaidTax = 0
b = startYear n b
pc = (+/ b[(not IsSP) sel iota count b]) * Pcr # platform charge
need = need + pc # add in platform charge
w = withdraw (need b) # withdrawn amounts that sum to need
t = taxOn w # calculate tax according to the tax regimes
UnpaidTax = +/ t # set UnpaidTax for payment next year.
b = endYear n b
(b - w) w t # end of year balance, withdrawals, and tax
# Return the balance after maxN years
# given the starting balances, withdrawals and taxes
# at the end of the previous 1...n years (n <= maxN).
op maxN years (n bs ws ts) =
b w t = n year bs[n] # balances, withdrawals and tax at the end of year n
bs = bs ,% b # append as row to bs
ws = ws ,% w # append as row to ws
ts = ts ,% t # append as row to ts
(n == maxN): bs ws ts # on reaching year maxN, return the accumulated rows.
maxN years (n+1) bs ws ts # otherwise recurse to return years (n+1) and above.
The work of calculating the effect of a single year is performed by the year operator. Given a starting balance array b (of length equal to the number of sources) and a year number n we calculate the end of year balance array, and return it with the withdrawal array and tax array.
The amount of income needed for the year is calculated by scaling up the Year1Income constant by the rate of inflation compounded over (n-1) additional years. To this we add any (unpaid) tax that was raised by withdrawals in the previous year, and the platform charges.
Unpaid tax is maintained in a global variable, a rather clumsy mechanism that requires that the year operator is called with consecutive values of n - which it is. The global UnpaidTax is initialised immediately above the year operator to stress its local nature.
The platform charge is determined as a percentage of the balance of the non-state pension sources.
The years operator recursively iterates through years from n up to maxN years (where n < maxN) calling year for each new value of n and appending the returned balance, withdrawal and tax arrays, b, w, and t, as new rows on the bs, ws, and ts matrices.
The end result is that the data for year n appears in the nth row of each of these matrices. Once we reach year n we return the completed matrices and no further recursion occurs.
Execution and the Output of CSV Data
# Unpack the year, source name, amount withdrawn, tax raised,
# and year-end balance for each combination of year and source.
op (n i) byYearSource (s bs ws ts) =
n s[i] ws[n;i] ts[n;i] bs[n;i]
op a csv b = (text a) , ',' , (text b)
# Run for n years with b as the opening balance.
op run (n b) =
bs = 1 (count b) rho b # matrix with b as the only row
ws = 0 (count b) rho 0 # empty matrix of the same shape
ts = 0 (count b) rho 0 # empty matrix of the same shape
bs ws ts = n years 1 bs ws ts
bs = 1 drop bs # drop the opening balance
year_source = , (iota n) o., (iota count S)
M = year_source @byYearSource S bs ws ts
print "Year, Source, Withdrawn, Tax Raised, Balance"
mix csv/mix M
run N BThe monadic operator run takes a single array parameter which contains two values: a number of years, n, for which to run the iteration, and an array, b, which contains the opening balance for each of the sources.
The aim of run is to use years to iterate over the given number of years using the starting balances. It does this by calling the dyadic operator years with a starting year of 1 and an ending year of n and capturing the returned matrices. The returned matrices contain the end of year balances, within year withdrawal amount, and within year tax amount. Year n data is in the nth row of each matrix.
There is a little trick in the bootstrapping of the balances array: the years operator expects to find the opening balances for year n in the nth row of the bs matrix that is passed to it as an argument. So we initialise bs with the passed in opening balances and then when years returns we drop the initial opening balance from bs so that it contains the closing balances for year n in the nth position and has a length of n - the same as the lengths of both ws and ts.
To output the CSV we use the monadic print operator to output our textual header. We construct a single array year_source that contains an entry for each combination of year (1 to n) and source index (1 to count S). We do this with the outer join operator o. applied to the catenation operator (dyadic ,) and then ravel the whole thing into a one-dimensional array with the ravel operator (monadic ,).
year_source = , (iota n) o., (iota count S)This gives us a vector that, for n = 30 and 4 sources, looks like this:
(1 1) (1 2) (1 3) (1 4) (2 1) (2 2) (2 3) (2 4) (3 1)...(30 4)We construct a dyadic operator byYearSource that takes one of these year-and-source tuples as its left argument and the source, balance, withdrawal, and tax matrices as its right argument and which returns a vector containing the values of the CSV data that we would like to see on each line Such a line would correspond to year n and source (index) i.
op (n i) byYearSource (s bs ws ts) =
n s[i] ws[n;i] ts[n;i] bs[n;i]We invoke “each left” on this operator to generate a matrix containing the CSV data that we would like to see in our output.
M = mix year_source @byYearSource S bs ws tsOur matrix M contains a row for each year and a column for each of the 5 data values returned by byYearSource - year, source name, withdrawal, tax and balance.
We reduce across the rows with our csv operator which gives us a vector with an element for each value of year_source and with the data values separated by a comma. We lay these out one per line by applying mix again.
mix csv/MWhere the csv operator is defined (above) as:
op a csv b = (text a) , ',' , (text b)Finally we invoke the run operator passing it, as values of n and b, the global constants N and B which were set near the top of the Ivy script.
The resultant text is printed to standard output and we capture it manually into a file, perhaps by invoking ivy from the shell, like this:
ivy drawdown.ivy >drawdown.csvThe output looks something like this:
Year, Source, Withdrawn, Tax Raised, Balance
1,State Pension 1,10000,0,0
1,State Pension 2,0,0,0
1,Pension,26475,4787,473525
1,GIA,0,0,50000
1,Savings,0,0,40000
2,State Pension 1,10250,0,0
2,State Pension 2,0,0,0
2,Pension,31695,5868,458404
...Such data can easily be read into a tool for analysis. Different outcomes can be modelled by changing the values of various constants and re-running the iteration:
N, to give the number of years on which to iterate.B, to modify the opening balances.Igr,Sgr,Inf,Pcr,Tbr, to see the effect of different rates.- The upper bounds and percentage tax rates of the different kinds of tax regime.
- The order in which income is withdrawn from the sources in
S(using the draw sequence inDS). - The state pension starting years and annual amounts and increases in
SPStartYear,SPY1andSPAPI.
More complicated scenarios can be modelled with the Go version of Drawdown.